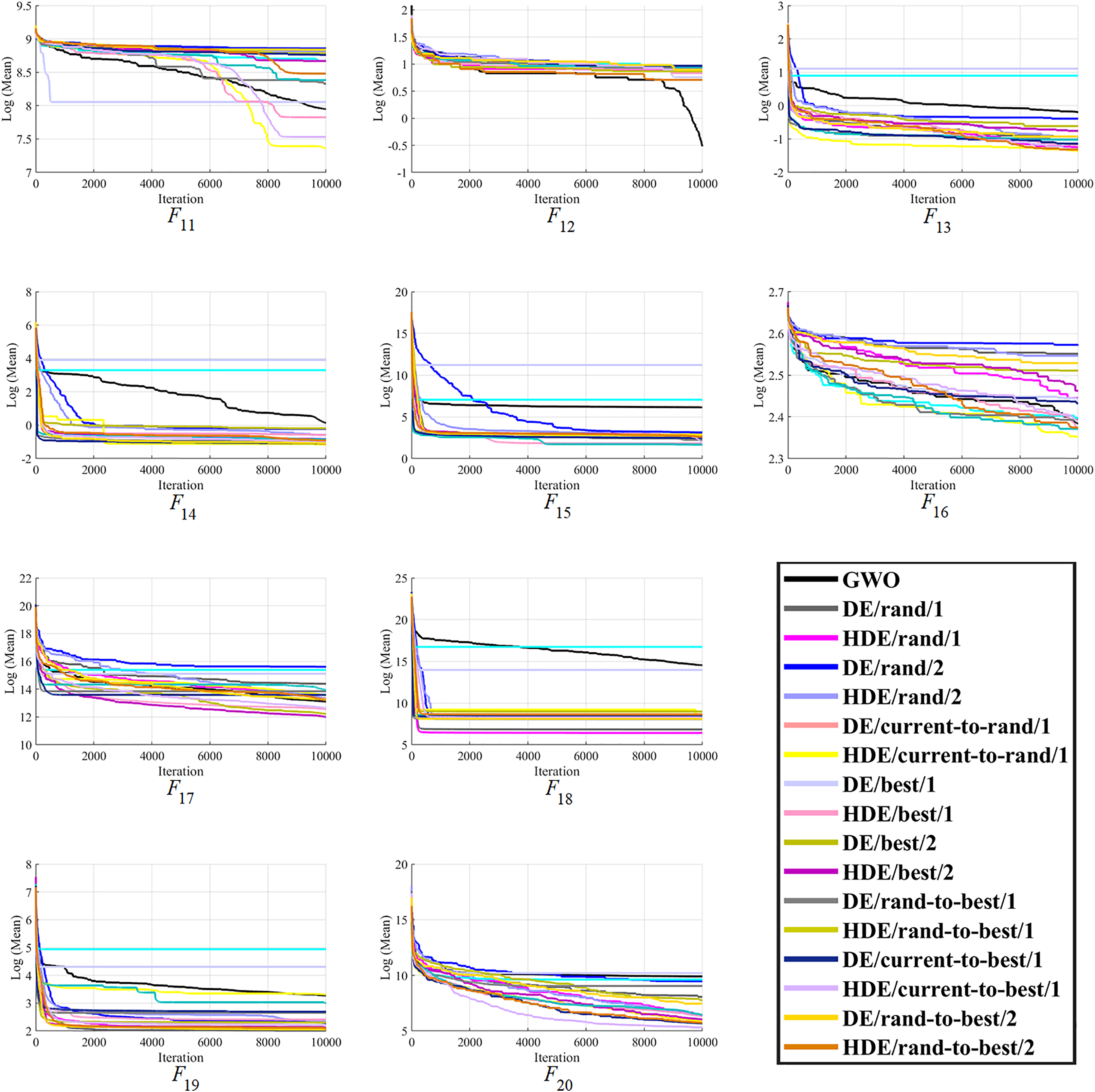
Differential evolution (DE) belongs to the most usable optimization algorithms, presented in many improved and modern versions in recent years. Generally, the low convergence rate is the main drawback of the DE algorithm. In this article, the gray wolf optimizer (GWO) is used to accelerate the convergence rate and the final optimal results of the DE algorithm. The new resulting algorithm is called Hunting Differential Evolution (HDE). The proposed HDE algorithm deploys the convergence speed of the GWO algorithm as well as the appropriate searching capability of the DE algorithm. Furthermore, by adjusting the crossover rate and mutation probability parameters, this algorithm can be adjusted to pay closer attention to the strengths of each of these two algorithms. The HDE/current-to-rand/1 performed the best on CEC-2019 functions compared to the other eight variants of HDE. HDE/current-to-best/1 is also chosen as having superior performance to other proposed HDE compared to seven improved algorithms on CEC-2014 functions, outperforming them in 15 test functions. Furthermore, jHDE performs well by improving in 17 functions, compared with jDE on these functions. The simulations indicate that the proposed HDE algorithm can provide reliable outcomes in finding the optimal solutions with a rapid convergence rate and avoiding the local minimum compared to the original DE algorithm.